Outperforming hash-tables with MICA
MICA: A Holistic Approach to Fast In-Memory Key-Value Storage Lim et. al., NSDI 2014
In this installment we’re going to look at a system from NSDI 2014. MICA is another in-memory key-value store, but in contrast to Masstree it does not support range queries and in much of the paper it keeps a fixed working set by evicting old items, like a cache. Indeed, the closest comparison system that you might think of when reading about MICA for the first time is a humble… hash table. Is there still room for improvement over such a fundamental data structure? Read on and find out (including benchmarks!).
The Big Idea
MICA is another key-value store, one that starts from a different set of assumptions to, for
example, Masstree, and as a result ends up at a rather different point in the design space. The
target environment is pretty similar: MICA is designed to take advantage of multi-core CPUs, and all
keys and values are stored in memory. Storage is limited to a single node - there’s no replication
or partitioning by distribution (although those could probably be added without changing much of
MICA as presented here). The data stored are string (key, value) pairs. But beyond those initial
similarities, there are some important differences:
No range queries
MICA supports get(key), put(key, value) and delete(key) operations, but does not support
getRange(low_key, high_key). This is a critical difference: if you don’t have to service range
queries you don’t have to index any information about the relative values of keys, and therefore
you don’t have to perform many comparisons on the read or write paths. In Masstree we saw that a lot
of effort went into optimizing comparisons by keeping them constant-cost. That shouldn’t be a focus
for a system like MICA.
Emphasis on cache semantics
MICA supports four operating modes (more on that later). The largest focus in the paper is on cache semantics, rather than store semantics, although implementations for both are provided. Cache semantics are easier to support than store semantics, because MICA can choose what data to retain in order to preserve performance and manage memory usage.
Keys and values are short
Masstree focused on long keys and values with potentially a high degree of prefix overlap. MICA instead assumes that keys and values are relatively short - short enough to fit into a UDP packet, so about 64k in total (and in fact the evaluation is performed with a total string length no longer than 1132 bytes). Shorter keys and values present their own difficulties: comparison costs are lower so perhaps not so important to focus on, but they also require small memory allocations which can lead to more fragmentation and higher overhead (e.g. the fixed cost of tracking an allocation becomes more significant with higher allocation volume).
One of MICA’s key design tenets is to think holistically to satisfy its design and performance goals. That means the authors allowed themselves to co-design the network layer and the storage data structures. The result is a design that’s pretty harmonious, with optimizations that were only available because they were able to make changes to all aspects of the system at once.
As far as performance goals go, MICA targets low end-to-end latency, consistent performance across workloads and high single-node throughput. How does it go about achieving them? Let’s start by looking at the data structures - but first we need to digress into MICA’s different ‘modes of operation’.
Operating modes
MICA has two different storage semantics that it implements:
- Cache mode has MICA behaving like a traditional in-memory cache, a la Memcache. A fixed amount of memory is used, and when more is needed, some old or less frequently used item is evicted to make room.
- Store mode is when MICA keeps all
(key, value)pairs in memory, growing the memory required to store them as required.
Roughly speaking, both cache and store modes have similar network stacks and data structure design, but the actual data structures used are a bit different to each other.
To complicate things further, each mode can operate in one of two ‘operating modes’ which describe how much coordination can be performed between cores. One of MICA’s design principles is to statically hash-partition keys between cores so that separate requests for keys in different partitions can be served in parallel with no locks or waiting. However, if one core is not enough to serve the load for its partition, MICA could end up bottlenecked on single-core throughput and may decide to serve read requests for a partition from other cores than the one that ‘owns’ the partition. MICA can be configured to use two different strategies:
- Exclusive-Read-Exclusive-Write (EREW) mode only allows the owning core to serve requests for its partition.
- Concurrent-Read-Exclusive-Write (CREW) mode allows other cores to serve
getrequests, but all updates are done by a single core.
To keep this write-up a manageable length, we mostly focus on MICA in EREW mode, implementing cache semantics, as this is the mode the paper devotes the most space to. There are lots of interesting details about the other three combinations, so go read the paper for the most detail.
Data structures, logs and hash tables
MICA identifies two main areas for improvement over traditional data structures like hash tables. These improvements lead the authors to split their data structures into two parts: the first to store the data in a memory-allocator-friendly fashion, and the second to index it efficiently.
Append-only in-memory storage
The first observation made by the authors is that memory allocation can be a problem for systems that have lots of relatively small writes. Dynamically allocating memory to data items as requests arrive can lead to fragmentation, affecting memory usage efficiency.
MICA addresses this by doing something pretty sensible: it writes all keys and values in succession to an append-only log data structure. You can think of this like a book where you just write anything new to last blank page. This way the keys and values fit perfectly, using no more memory than they need. Finding a key-value pair just involves knowing the location (i.e. the page number) in this log where it was written, and so looking it up is \(O(1)\).
This all sounds great, but of course it has an obvious drawback: the more you write to the log, the more memory it uses. If all you are doing is writing new keys, that might be an acceptable behavior if you’re trying to keep all the data in memory, but if you are updating the value for an already existing key, you have two choices: you can try to overwrite it in place, or you can append the new value to the log and update the recorded offset.
The former works well up until your new value is longer than the original, then you can’t update in place because you’ll corrupt the data that was written immediately afterwards. So in general, you have to append updates. But then you’ve got two entries in the log for one key, and the ‘earlier’ one is out of date and wasting space. So this system needs some kind of garbage collection.
Garbage collection of a log-structured record is an old problem, discussed in the context of filesystems at least 25 years ago. There are lots of pretty obvious approaches - you can snapshot the log to a more compact representation and then start a brand new log, you can compact the log in-place by rewriting it with out-of-date entries removed, or you can do what MICA does which is just… overwrite old items in a FIFO manner.
MICA simply wraps the log when it reaches its maximum length and starts writing from the beginning again. Remember that we’re focusing on cache mode, so ‘evicting’ (i.e. deleting) old items is a legitimate thing for the system to do. This relaxed requirement (over store-mode) allows MICA to make this very simple optimisation. Now all memory is used to hold key-value pairs (once the log is full), the amount of memory used by a MICA instance is controllable, and although there is still wasted space, the advantage over dynamic allocation is that the waste doesn’t lead to fragmentation, so doesn’t impede the ability of the allocator to find a good-sized allocator.
FIFO is a bit of a weird order to evict items, since it’s independent of how frequently used a key is. A more traditional eviction order is Least-Recently Used (LRU), which MICA can approximate by re-appending an item when it is accessed to the end of the log. Moving it to the end of the log ensures that it’s the last entry to be overwritten when the log wraps around. There are some questions raised by this approach - it’s effectively ensuring that every item will be written more than once to each log, and a workload that e.g. interleaves requests for two different keys will eventually cause the log to be full of those keys only, having overwritten every other entry. MICA’s evaluation is conducted in this approximate-LRU mode, so we can infer it doesn’t have too problematic an effect when the key + value size is very small in comparison to the log size.
Lossy hash tables
Armed with an efficient, allocation-free storage data structure to retain key-value pairs, all that remains is to provide a similarly efficient data structure to index the log, by making it fast to lookup the offset of any key in the log.
Just to recap, the idea is that, when performing a get(key) operation, MICA will use its index
data structure to find an offset for that key in the in-memory log. It will then perform a
log.read(key, offset) operation to return the value if it exists.
There are lots of off-the-shelf data structures that we could use - again, a hash table would suffice. The paper claims that traditional implementations are typically too slow for writes, being read-optimized; and write-friendly structures like chained hash tables are too slow for reads.
Instead, MICA proposes a hash-table variant that is fast for both reading and writing. The basic idea is very similar to chained hash tables, in that items that collide in the same bucket are stored together (rather than probed tables, where one item has to go look for another bucket). The difference is that, instead of forming a linked-list out of colliding elements, MICA allocates a fixed amount of memory to each bucket that can hold a small number of entries. If there’s no room in that bucket, MICA will - again - evict some entry.
The advantage is that, by grouping together the colliding entries in memory in a single ‘bucket’, it becomes very efficient to search the set of colliding elements for a match when doing a lookup operation. Linked lists are notoriously inefficient at using the memory bus because every step in the chain is a dependent memory read - i.e. it depends on the node currently being looked at, so there’s no possibility of prefetch or parallel reads. Here, the location in memory of each entry in a bucket is known as soon as the bucket is read, so each entry in the bucket can be read in parallel.
To make this work best, the data stored in each entry must be of fixed size (otherwise you have
another dependent memory read to do to read, e.g., an unbounded string). What MICA does is compute a
‘tag’ of the key, which is a fixed-size subset of the hash of the key, and store that rather than
the key. So the basic data that needs to be stored for each write is an (offset, tag) pair. That
tag can be compared to a tag computed by the same process on any key that is being looked up; if the
tag isn’t found in the hash table, the key is not present in the underlying log.
(One aside is that MICA must handle the possibility of duplicate tags for different keys in a single bucket - the easiest solution is to overwrite any existing entry with the same tag when performing a write to maintain an invariant that there is at most one entry with a given tag in a bucket).
The idea of using a tag to make a hash table entry fixed-size is not new, and indeed is heavily used by a previous system from the same lab called SILT. In this context, the new idea appears to be allowing MICA to evict items as needed to ensure fixed-size buckets. This is what gives this data structure its ‘lossy’ name.
Parallelism: partitioning vs coordination
One of the major design decisions in MICA is to achieve parallelism by partitioning work across multiple cores by partitioning the keyspace across cores using hash-partitioning. Each core maintains its own private data structures and doesn’t need to read or write any other cores’ data. If done correctly, this can be an embarassingly parallel implementation with little or no coordination required between cores, but the potential downside is that, since each operation can only be processed by one core, any imbalance in workload will lead to imbalanced core utilization and poor efficiency. The opposite philosophy is to allow any core to service any request and to embrace the coordination that this requires; Masstree took this approach.
Workload skew is pretty much an accepted fact of life, so how does MICA justify or mitigate the per-core imbalance that results? The answer is in section 4.1.1. Firstly keys are hashed to map them to a core; this can spread the load from a popular range of keys, but does nothing when one key gets particularly hot.
MICA can take advantage of a natural optimization that happens when load on a particular partition is high: the network layer can batch delivery of many operations at once (up to 32 at a time). Apparently the per-packet overhead of managing the delivery queue is high, so amortizing that across 32 packets at once is a significant win.
It’s hard to know how reasonable these claims are. There’s an interplay between CPU and network efficiency which isn’t really called out. In order for batching to be effective, requests have to arrive more frequently than the CPU can read them from the network queue. So batching doesn’t help until the core is tapped out.
The point being that you could have a core processing 100 requests/s or more because of your amazing optimized data structures, and the observed latency is still lower than if those requests were spread across multiple cores (at perhaps a slightly higher cost / operation).
If the CPU is slower than the arrival rate, then batching causes the per-operation cost to go down (the network queue interaction cost is divided by 32). So the throughput of that core goes up, but the increase has to be larger than the ratio of workload it is receiving in order for it to break even (if the only CPU processing that was done was to read a packet from the network queue, the throughput would increase by 32x, therefore this is a win if a non-batched core is processing 32x fewer operations or more).
The evaluation of MICA shows that Zipfian skew causes throughput per-core to drop as the number of cores increases, but not precipitously up to 15 cores. An interesting data point is that per-core throughput is higher for the skewed load at one core, which is presumably the recipient of most load. Assuming that the cores were being 100% used, this points to the benefits of data locality when serving skewed workloads. The aggregate throughput across all cores, however, is lower for the skewed workload.
Partitioning without any coordination
It’s all well and good to have data structures that don’t need coordination, but you need a way to get work to those data structures, and their owning cores, in the first place without incurring heavy coordination overhead. This is easier said than done - think about how you might implement this naively. When a request comes in, some part of the system has to decide what core it goes on (computes the hash value), and then it has to deliver it to that core by writing to some queue. The problem is that the core that computes the hash value is unlikely to be the one that should process the request - there’s no way of knowing which core should process a request until the key is hashed - so it’s also possible that many threads at once could try to write to the core’s inbound request queue. This requires coordination. Coordination kills parallelism.
MICA uses a cool strategy to try to work around this. Because MICA is designed holistically, the authors very legitimately consider the client to be part of the system. And clients operate in parallel - so why not have them compute the hash value and then ‘send’ the request to the right core?
Since a client can know the number of MICA partitions \(N\) running on the server - it’s easy to do this when it connects, the number of partitions is going to be fixed and unchanging - it knows the right range \([0..N]\) for the hash value to take. So that part’s easy. The tricky part is addressing cores on a remote machine somehow.
The way this is done is to assign a UDP port to each core. The client can map a hash value to a port, and then packets sent to that port are delivered directly to that core, with next-to-no coordination required on the client or the server!
Each core has its own receive queue, managed for it by DPDK and accessible to user-space logic (i.e. MICA). As discussed earlier, each queue can deliver packets to each core efficiently by taking advantage of bulk delivery during times of high load.
How is this better than a hash table?
MICA’s evaluation shows, as you would expect, that it outperforms other systems for common workloads. The other systems include Memcache, Masstree, RAMCloud and MemC3.
I was interested in how MICA compared to more traditional data structure implementations, so I wrote a simple implementation of the data structures underpinning MICA’s EREW + cache mode, with both a circular log for storage and a lossy hash table for indexing. I called this implementation Formica, as it feels kind of cheap :)
Formica is available on Github. It might be interesting to look at to help with the paper, but don’t even think about using it as the basis for anything important!
Formica also contains two other in-memory key-value stores for comparison:
-
StdMapStoreuses a…std::mapas a non-lossy index into a Formica’s circular log. -
ChainedLossyHashStoreis a chained hash table that stores the data directly in the chain nodes. It is lossy because the chain lengths are fixed, and when a node needs to be evicted, the end of the chain is removed (new entries are inserted at the front).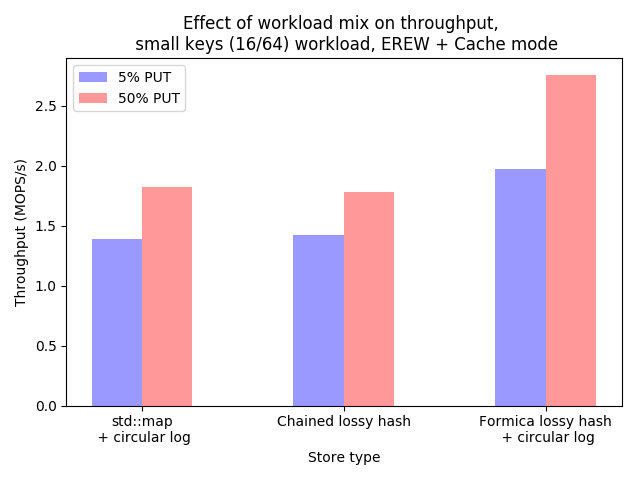
Throughput for MICA’s small-key test
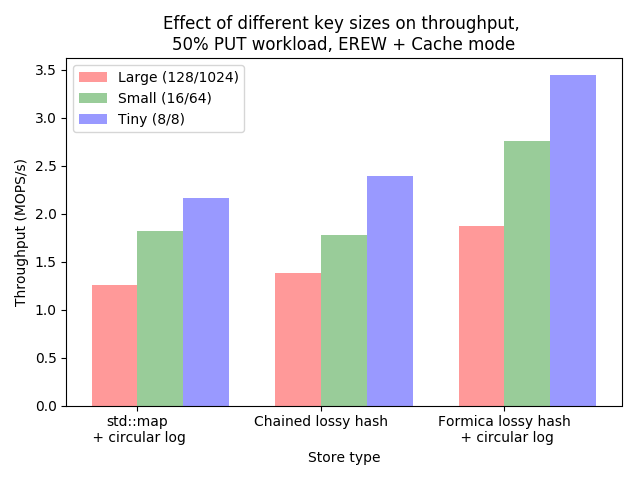
Throughput for various key sizes
We can see that Formica achieves better throughput than either of the other indexes. This benchmark only runs on a single core (on my 2013 Macbook Pro). That’s because I only want to test the effectiveness of MICA’s new data structures, not the virtues of their partition-not-coordinate design principle (note all three of the implementations are coordination-free, so we have to parallelise by keeping a private copy of each data structure per-thread). Therefore there’s also no skew in the workload, which was about 10 million operations on a pre-loaded data set of 2 million strings.
PUT operations are cheaper than GETs (and this continues if the mix of PUTs is turned up even
higher), presumably because there aren’t as many, if any, full-key comparisons on the write path.
The data structures were sized to keep cache misses due to eviction to around 0-5%. The circular log, where used, was large enough to hold almost all the written keys and values but it was much harder to size the hash tables correctly. For Formica, each bucket in the table had about 25 entries, which means that to store 2M keys would need about 84k buckets. You should take these benchmark results with a huge grain of salt since I didn’t have time to really dig into every observation to make sure I understood it, but I believe that the general trend is accurate.
And that general trend is that… Formica (and thus MICA) is a superior design for single-core
throughput for a key-value in-memory cache. It’s particularly interesting that the fixed-size bucket
hash table beats out the chained version quite handily. The chained version doesn’t do any memory
allocation after the chains get full, so the cost is likely to be doing the dependent reads walking
the linked list during GETs. Indeed, when the mix of GETs is reduced to about 5%, the
performance of the chained hash table increases significantly.
So data structure choices do continue to matter. Don’t forget that anytime anyone asks you what the point is in learning how to walk a binary tree.